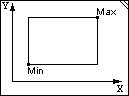
Для неё достаточно будит дистанцию каждых точек друг от друга :)
Function CubeVsPoint(Box,Point :TVector; Size:Single):Boolean;
Begin
If (abs(Point.x - Box.x)< Size) And
(abs(Point.y - Box.y)< Size) And
(abs(Point.z - Box.z)< Size) Then Result := True Else Result := False;
end;

Её же можно переделать в проверку с ящиком (Вариант 1):
Function BoxVsPoint(Box,BoxSize,Point :TVector):Boolean;
Begin
IF (abs(Point.x - Box.x)< BoxSize.x) And
(abs(Point.y - Box.y)< BoxSize.y) And
(abs(Point.z - Box.z)< BoxSize.z) Then Result := True Else Result := False;
end;
Проверка ящика с точкой (Вариант 2):function AABBVsPoint(Minx,Maxx,Pos :TVector): boolean; begin IF (Pos.X >= Minx.X) and (Pos.X <= Maxx.X) and (Pos.y >= Minx.y) and (Pos.y <= Maxx.y) and (Pos.z >= Minx.z) and (Pos.z <= Maxx.z) then result := true else result:=false; end;
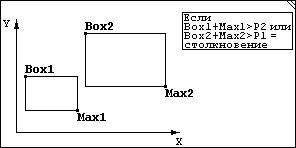
Ну а это проверка двух ящиков с разными размерами
function AABBVsAABB(Box1, Box2, Box1Size, Box2Size :TVector): boolean;
begin
if (box1.X + box1size.X < Box2.X) or
(box1.y + box1size.y < Box2.y) or
(box1.z + box1size.z < Box2.z) or
(Box2.x + box2size.X < box1.X) or
(Box2.y + box2size.y < box1.y) or
(Box2.z + box2size.z < box1.z) then
Result:=false else result:=true;
end;

Проверка ящика со сферой:
function AABBVsSphere(Minx,Maxx,Pos :TVector;R:Single): boolean;
var
d :single;
begin
d := 0;
// если центр сферы лежит перед AABB,
if (Pos.x < Minx.x) then
// то вычисляем расстояние по этой оси
d:=d+ abs(Pos.x - Minx.x);
// если центр сферы лежит после AABB,
if (pos.x > Maxx.x) then
// то вычисляем расстояние по этой оси
d:=d+ abs(Pos.x - Maxx.x);
(******************************************************************************)
if (Pos.y < Minx.y) then d :=d + abs(Pos.y - Minx.y);
if (pos.y > Maxx.y) then d :=d + abs(Pos.y - Maxx.y);
(******************************************************************************)
if (Pos.z < Minx.z) then d :=d + abs(Pos.z - Minx.z);
if (pos.z > Maxx.z) then d :=d + abs(Pos.z - Maxx.z);
(******************************************************************************)
result := d <= ( R);
end;
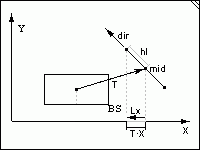
Проверка линии с кубом:
function CubeVsLine(BP,LBEGIN,LEND:TVector;BS :single): boolean; Var MID, DIR, T : TVector; HL, R : Single; begin // Получаем центр Mid.x := lbegin.x+(lend.x-lbegin.x)*0.5; Mid.y := lbegin.y+(lend.y-lbegin.y)*0.5; Mid.z := lbegin.z+(lend.z-lbegin.z)*0.5; // Получаем направление dir.x := (lend.x-lbegin.x); dir.y := (lend.y-lbegin.y); dir.z := (lend.z-lbegin.z); // Получаем длину hl := sqrt(sqr(dir.x)+sqr(dir.y)+sqr(dir.z)); // Нормализуем её if hl <> 0 then begin dir.x := dir.x / hl; dir.y := dir.y / hl; dir.z := dir.z / hl; hl := hl * 0.5; end; // Получаем позицию куба относительно середины линии t.x := BP.x -mid.x; t.y := BP.y -mid.y; t.z := BP.z -mid.z; // проверяем, является ли одна из осей X,Y,Z разделяющей if ( (abs(T.x) > BS + hl*abs(dir.x)) or (abs(T.y) > BS + hl*abs(dir.y)) or (abs(T.z) > BS + hl*abs(dir.z)) ) then begin result := false ; exit; end; // проверяем X ^ dir r := BS*abs(dir.z) + BS*abs(dir.y); if ( abs(T.y*dir.z - T.z*dir.y) > r ) then begin result := false ; exit; end; // проверяем Y ^ dir r := BS* abs(dir.z) + BS* abs(dir.x); if ( abs(T.z*dir.x - T.x*dir.z) > r ) then begin result := false ; exit; end; // проверяем Z ^ dir r := BS*abs(dir.y) + BS*abs(dir.x); if ( abs(T.x*dir.y - T.y*dir.x) > r ) then begin result := false ; exit; end; result := true; end;
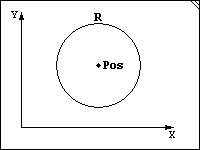
Простая проверка сферы с точкой:
Просто проверяем дистанция меньше до сферы меньше ли радиуса ? если да то столкновение есть :)
function SphereVsPoint(Sphere,Point :TVector; R: Single): boolean; Var dist: Single; begin // Получение дистанции мужду двумя точками dist:=sqrt(sqr(Sphere.X-Point.X)+sqr(Sphere.Y-Point.Y)+sqr(Sphere.Z-Point.Z)); // Если она меньше радиуса сферы то есть столкновение if dist<=R then result:=true else result:=false; end;

Проверка двух сфер:
Function SphereVsSphere(Sphere1,Sphere2 : TVector; R1,R2 : Single) : boolean; Var R,RR : Single; X,Y,Z : Single; begin R:= (R1 + R2); //Получем центр и радиус X := Sphere2.x - Sphere1.X; Y := Sphere2.Y - Sphere1.Y; Z := Sphere2.Z - Sphere1.Z; rr := sqrt(x*x +y*y +z*z); if rr < r then Result := True else Result := false; // если r больше rr то нет столкновения end;Проверка сфера с линией :
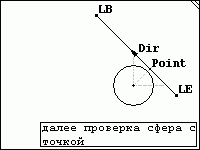
function SphereVsLine(Sphere, LB,LE : TVector;R: Single): boolean; var Point, Vector1, Vector2, Dir : TVector; D, T : Single; begin Result :=false; // Узнаём положение сферы относительно начала линии Vector1.x := Sphere.x - Lb.x; Vector1.y := Sphere.y - Lb.y; Vector1.z := Sphere.z - Lb.z; // Узнаём направление Dir.x := Le.x - Lb.x; Dir.y := Le.y - Lb.y; Dir.z := Le.z - Lb.z; // Узнаём длину D := sqrt(sqr(Dir.X) + sqr(Dir.Y) + sqr(Dir.Z)); // Нормализируем её if d >0 then begin Vector2.x := Dir.x * 1/d; Vector2.y := Dir.y * 1/d; Vector2.z := Dir.z * 1/d; end; // Узнаём дистанцию между началом и концом линии d := sqrt(sqr(Le.X - LB.X) + sqr(Le.Y - LB.Y) + sqr(Le.Z - LB.Z)); // Перемножаем их и получаем приделы линии где может быть сфера t := (Vector1.X * Vector2.X) + (Vector1.Y * Vector2.Y) + (Vector1.Z * Vector2.Z); // Вышли за приделы линии if t+r <= 0 then Exit; if t-r >= d then Exit; // Получаем местоположение сферы относительно линии Point.x := lb.x + Vector2.x* t; Point.y := lb.y + Vector2.y* t; Point.z := lb.z + Vector2.z* t; // Получаем дистанцию между сферой и точкой .. // Если она меньше радиуса сферы то есть столкновение if sqrt(sqr(Sphere.x-Point.x)+sqr(Sphere.y-Point.y)+sqr(Sphere.z-Point.z)) <=R then Result := true; end;Вы можете скачать этот готовый пример с сайта: Проверка столкновений